ऑटोमेटाचा सिद्धांत, मर्यादित ऑटोमेटा

विविध मशीन्सची रचना, रचना, ऑपरेशनचे तत्त्व मुख्यत्वे त्याच्या कार्यात्मक उद्देशाने निर्धारित केले जाते. तांत्रिक, वाहतूक, संगणन, लष्करी आणि इतर मशीनमधील फरक ओळखा. जटिल तांत्रिक प्रक्रिया करण्यासाठी डिझाइन केलेले संपूर्ण स्वयंचलित कॉम्प्लेक्स विविध उद्योगांमध्ये मोठ्या प्रमाणावर सादर केले जातात. ऑटोमेटाची रचना आणि बांधणी केली जाते जी विविध तार्किक कार्ये (लॉजिकल मशीन) करतात.

ऑटोमेटाचा सिद्धांत — सायबरनेटिक्स विभाग, जे डिजिटल संगणक आणि नियंत्रण मशीनच्या तंत्रज्ञानाच्या आवश्यकतांच्या प्रभावाखाली उद्भवले. ऑटोमेटा थिअरीमध्ये अभ्यासलेले डिस्क्रिट ऑटोमेटा हे रिअल सिस्टीमचे (तांत्रिक आणि जैविक दोन्ही) अमूर्त मॉडेल आहेत जे वेगळ्या (डिजिटल) माहितीवर वेगळ्या वेळेच्या चरणांवर प्रक्रिया करतात.

ऑटोमॅटा सिद्धांत अचूक गणितीय संकल्पनांवर आधारित आहे जे ऑटोमॅटनच्या कार्य (वर्तन) आणि त्याच्या संरचनेबद्दल (अंतर्गत रचना) अंतर्ज्ञानी कल्पनांना औपचारिक बनवते.

या प्रकरणात, माहितीचे परिवर्तन नेहमीच एक ऑपरेशन म्हणून समजले जाते जे इनपुट वर्णमालामधील अक्षरे बनलेल्या इनपुट अनुक्रमांचे आउटपुट वर्णमालामधील अक्षरे बनलेल्या आउटपुट अनुक्रमांमध्ये रूपांतरित करते.

गणितीय तर्कशास्त्र, बीजगणित, संभाव्यता सिद्धांत, संयोजनशास्त्र आणि आलेख सिद्धांत यांचे उपकरण मोठ्या प्रमाणावर वापरले जाते.

ऑटोमेटाच्या काही भागांमध्ये (ऑटोमेटाचा स्ट्रक्चरल सिद्धांत) समस्या वाढली रिले-संपर्क सर्किटच्या सिद्धांतावरून, जे 1930 च्या उत्तरार्धात आकार घेऊ लागले. समावेशक तार्किक बीजगणित पद्धती.

ऑटोमेटाच्या स्ट्रक्चरल सिद्धांतामध्ये, वेगवेगळ्या प्रकारच्या योजनांचा अभ्यास केला जातो, ज्याची रचना प्रणालीमध्ये योग्यरित्या जोडलेल्या सोप्या घटकांपासून (घटकांपासून) जटिल ऑटोमॅटन ​​कसे तयार केले जाते याचे वर्णन केले जाते.

ऑटोमेटाचा अमूर्त सिद्धांत नावाची दुसरी दिशा, ऑटोमेटाच्या वर्तनाचा अभ्यास करते (म्हणजेच, त्यांच्याद्वारे केलेल्या माहितीच्या परिवर्तनाचे स्वरूप), त्यांच्या अंतर्गत संरचनेच्या वैशिष्ट्यांचे अमूर्तीकरण करताना, आणि 1950 च्या दशकात उद्भवली.

ऑटोमेटाच्या अमूर्त सिद्धांताच्या चौकटीत, "ऑटोमॅटन" आणि "मशीन" या संकल्पनांची सामग्री अनिवार्यपणे ऑटोमॅटनद्वारे केलेल्या माहितीच्या परिवर्तनाच्या मानक वर्णनाद्वारे संपली आहे. असे परिवर्तन निश्चित असू शकते, परंतु ते निसर्गात संभाव्य देखील असू शकते.

सर्वात जास्त अभ्यास केले गेलेले निर्धारक मशीन्स (ऑटोमॅटा), ज्यामध्ये मर्यादित ऑटोमेटा समाविष्ट आहे - ऑटोमेटाच्या सिद्धांतातील अभ्यासाचा मुख्य विषय.

मर्यादित स्थितीचे मशीन मर्यादित प्रमाणात मेमरी (अंतर्गत स्थितींची संख्या) द्वारे वैशिष्ट्यीकृत केले जाते आणि संक्रमण कार्य वापरून परिभाषित केले जाते.काही वाजवी आदर्शीकरणासह, सर्व आधुनिक गणिती यंत्रे आणि अगदी मेंदू, त्यांच्या कार्याच्या दृष्टिकोनातून, मर्यादित ऑटोमेटा म्हणून ओळखले जाऊ शकते.

"सिक्वेंशियल मशीन", "मिली ऑटोमॅटन", "मूर ऑटोमॅटन" हे शब्द साहित्यात वापरले जातात (आणि सर्व लेखकांनी एकसमान नाही) "परिमित ऑटोमॅटन" या शब्दाचे समानार्थी शब्द म्हणून किंवा मर्यादित च्या संक्रमण कार्यांमध्ये विशिष्ट वैशिष्ट्यांवर जोर देण्यासाठी वापरले आहेत. ऑटोमॅटन

अमर्यादित मेमरी असलेले ऑटोमेटा हे एक ट्युरिंग मशीन आहे जे कोणतेही कार्यक्षम माहिती परिवर्तन (संभाव्यपणे) करण्यास सक्षम आहे. "ट्युरिंग मशीन" ची संकल्पना "फिनिट स्टेट मशीन" च्या संकल्पनेपेक्षा पूर्वी उद्भवली आणि मुख्यतः अल्गोरिदमच्या सिद्धांतामध्ये त्याचा अभ्यास केला जातो.

अमूर्त ऑटोमेटा सिद्धांत सुप्रसिद्ध बीजगणित सिद्धांतांशी जवळचा संबंध आहे, उदाहरणार्थ अर्धसमूह सिद्धांत. लागू केलेल्या दृष्टिकोनातून, मेमरी आकाराच्या दृष्टीने ऑटोमॅटनमधील माहितीचे परिवर्तन दर्शविणारे परिणाम स्वारस्यपूर्ण आहेत.

हे असे आहे, उदाहरणार्थ, ऑटोमॅटावरील प्रयोगांच्या समस्यांमध्ये (ई. एफ. मूर इ. कार्य करते), जेथे ऑटोमॅटनच्या संक्रमण कार्यांबद्दल किंवा त्याच्या मेमरीच्या क्षमतेबद्दल एक किंवा दुसरी माहिती प्राप्त होते. प्रयोग

ऑटोमॅटनच्या मेमरी आकार आणि इनपुट अनुक्रमांच्या कालावधीबद्दल उपलब्ध माहितीच्या आधारे आउटपुट अनुक्रमांच्या कालावधीची गणना करणे हे दुसरे कार्य आहे.

मर्यादित राज्य मशीनची स्मृती कमी करण्यासाठी आणि यादृच्छिक वातावरणात त्यांच्या वर्तनाचा अभ्यास करण्यासाठी पद्धतींचा विकास करणे हे खूप महत्वाचे आहे.

अमूर्त ऑटोमेटा सिद्धांतामध्ये, संश्लेषण समस्या खालीलप्रमाणे आहे.काही स्पष्टपणे औपचारिक भाषेच्या संदर्भात, अटी डिझाइन केलेल्या ऑटोमॅटनच्या वर्तनासाठी (ऑटोमॅटनमध्ये दर्शविलेल्या कार्यक्रमासाठी) लिहिल्या जातात. या प्रकरणात, प्रत्येक लिखित स्थितीनुसार पद्धती विकसित करणे आवश्यक आहे:

1) असे राज्य मशीन अस्तित्वात आहे की नाही ते शोधा की त्याद्वारे बदललेली माहिती ही अट पूर्ण करते;

2) होय असल्यास, अशा मर्यादित स्थिती मशीनची संक्रमण कार्ये तयार केली जातात किंवा त्याच्या मेमरी आकाराचा अंदाज लावला जातो.

अशा फॉर्म्युलेशनमधील संश्लेषण कार्याचे निराकरण म्हणजे रेकॉर्डिंगपासून संक्रमणात्मक फंक्शन्समध्ये संक्रमणासाठी सोयीस्कर अल्गोरिदमसह ऑटोमॅटनच्या ऑपरेटिंग परिस्थिती रेकॉर्ड करण्यासाठी सोयीस्कर भाषेची प्राथमिक निर्मिती अपेक्षित आहे.

ऑटोमेटाच्या स्ट्रक्चरल सिद्धांतामध्ये, संश्लेषणाच्या समस्येमध्ये दिलेल्या प्रकारच्या घटकांची साखळी तयार करणे समाविष्ट आहे जे त्याच्या संक्रमण कार्यांद्वारे दिलेले मर्यादित ऑटोमॅटन ​​लक्षात घेते. या प्रकरणात, ते सहसा काही इष्टतमतेचे निकष (उदाहरणार्थ, घटकांची किमान संख्या) नमूद करतात आणि इष्टतम योजना मिळविण्याचा प्रयत्न करतात.

हे नंतर दिसून आले, याचा अर्थ रिले-संपर्क सर्किट्सच्या संबंधात पूर्वी विकसित केलेल्या काही पद्धती आणि संकल्पना दुसर्‍या प्रकारच्या सर्किट्सना लागू आहेत.

इलेक्ट्रॉनिक तंत्रज्ञानाच्या विकासाच्या संबंधात, सर्वात व्यापक योजना आहेत कार्यात्मक घटकांचे (तार्किक नेटवर्क). लॉजिक नेटवर्कचे एक विशेष प्रकरण म्हणजे अमूर्त न्यूरल नेटवर्क, ज्याच्या घटकांना न्यूरॉन्स म्हणतात.

संश्लेषणाच्या अनेक पद्धती विकसित केल्या गेल्या आहेत, सर्किट्सच्या प्रकारावर आणि माहितीचे परिवर्तन ज्यासाठी त्यांचा हेतू आहे (रिले उपकरणांचे संश्लेषण).

दिसत -कॉम्बिनेशनल सर्किट्स, कार्नोट नकाशे, सर्किट संश्लेषण कमी करणे

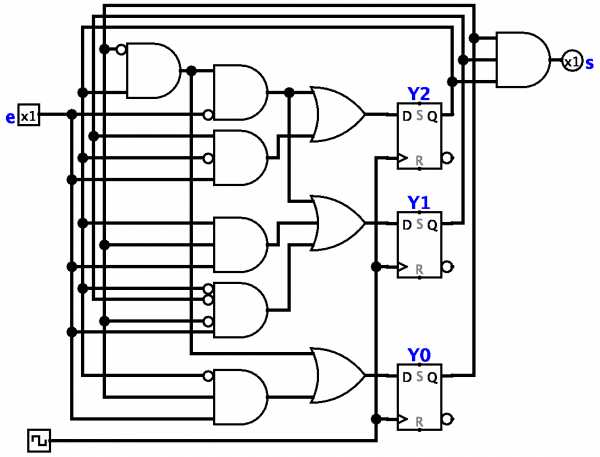
मर्यादित राज्य मशीन - स्थिर (ऑपरेशन दरम्यान वाढण्यास अक्षम) मेमरी आकारासह नियंत्रण प्रणालीचे गणितीय मॉडेल.

मर्यादित राज्य मशीनची संकल्पना ही एक गणितीय अमूर्तता आहे जी नियंत्रण प्रणालीच्या संचाची सामान्य वैशिष्ट्ये दर्शवते (उदाहरणार्थ, मल्टी-लूप रिले डिव्हाइस). अशा सर्व प्रणालींमध्ये सामान्य वैशिष्ट्ये आहेत जी मर्यादित ऑटोमॅटनची व्याख्या म्हणून स्वीकारणे स्वाभाविक आहे.

प्रत्येक पूर्ण झालेल्या ऑटोमॅटनमध्ये बाह्य प्रभाव आणि अंतर्गत घटकांच्या संपर्कात असलेले प्रवेशद्वार असते. इनपुट आणि अंतर्गत घटक या दोन्हीसाठी, विशिष्ट अवस्थेची एक निश्चित संख्या आहे जी ते घेऊ शकतात.

इनपुट आणि अंतर्गत घटकांच्या स्थितीत बदल वेळेत वेगळ्या क्षणी होतो, ज्या दरम्यानच्या अंतरांना टिक्स म्हणतात. टेपच्या शेवटी अंतर्गत स्थिती (इंटर्नल्सची स्थिती) संपूर्णपणे अंतर्गत स्थिती आणि टेपच्या सुरूवातीस इनपुटची स्थिती द्वारे निर्धारित केली जाते.

मर्यादित ऑटोमॅटनच्या इतर सर्व व्याख्या या वैशिष्ट्यापर्यंत कमी केल्या जाऊ शकतात, विशिष्ट व्याख्येमध्ये जे गृहीत धरतात की मर्यादित ऑटोमॅटनचे उत्पादन आहे जे दिलेल्या वेळी ऑटोमॅटनच्या अंतर्गत स्थितीवर अवलंबून असते.

अशा वैशिष्ट्याच्या संदर्भात, त्याच्या इनपुट आणि अंतर्गत अवस्थांचे स्वरूप संपूर्ण ऑटोमॅटनच्या वर्णनाशी अप्रासंगिक आहे. इनपुट आणि राज्यांऐवजी, तुम्ही फक्त त्यांची संख्या यादृच्छिक क्रमांकनमध्ये पाहू शकता.

स्टेट मशीन सेट केले जाईल जर त्याच्या अंतर्गत स्टेट नंबरचे मागील अंतर्गत स्टेट नंबर आणि मागील इनपुट स्टेट नंबरवर अवलंबून असेल. असे कार्य अंतिम सारणीच्या स्वरूपात असू शकते.

संपूर्ण ऑटोमॅटन ​​परिभाषित करण्याचा आणखी एक सामान्य मार्ग म्हणजे तथाकथित बांधकाम संक्रमण आकृती. इनपुट स्थितींना सहसा फक्त इनपुट म्हटले जाते आणि अंतर्गत अवस्था ही फक्त अवस्था असतात.

मर्यादित राज्य मशीन हे दोन्ही तांत्रिक उपकरणांचे आणि काही जैविक प्रणालींचे मॉडेल असू शकते. पहिल्या प्रकारातील ऑटोमेटा, उदाहरणार्थ, रिले उपकरणे आणि विविध इलेक्ट्रॉनिक संगणक, समावेश. प्रोग्राम करण्यायोग्य तर्क नियंत्रक.

रिले उपकरणाच्या बाबतीत, रिले उपकरणाच्या संवेदनशील घटकांच्या राज्यांच्या संयोगाने इनपुट अवस्थांची भूमिका बजावली जाते (अशा राज्यांचे प्रत्येक संयोजन एक "जटिल अवस्था" असते, ज्याचे सर्व संवेदनशील घटकांचे संकेत असतात. हे वेगळे सांगते की त्यांच्याकडे दिलेल्या क्षणी आहे). त्याचप्रमाणे, रिले उपकरणाच्या मध्यवर्ती घटकांच्या अवस्थांचे संयोजन अंतर्गत अवस्था म्हणून कार्य करते.

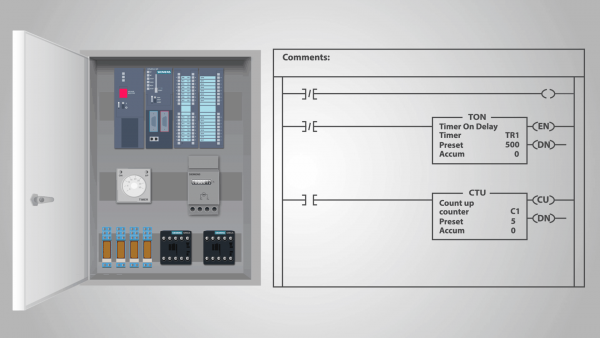
प्रोग्रामेबल लॉजिक कंट्रोलर (PLC) हे रिले अॅक्शन डिव्हाइसचे उदाहरण आहे ज्याला स्टँड-अलोन स्टेट मशीन म्हटले जाऊ शकते.

खरं तर, एकदा प्रोग्राम PLC मध्ये प्रविष्ट केला गेला आणि कंट्रोलरने गणना करण्यास सुरुवात केली की, तो बाह्य प्रभावांना सामोरे जात नाही आणि त्यानंतरची प्रत्येक स्थिती त्याच्या मागील स्थितीद्वारे पूर्णपणे निर्धारित केली जाते. आपण असे गृहीत धरू शकतो की प्रत्येक घड्याळाच्या चक्रामध्ये इनपुटची स्थिती समान असते.

याउलट, केवळ संभाव्य इनपुट स्थिती असलेल्या कोणत्याही मर्यादित राज्य मशीनला नैसर्गिकरित्या स्वायत्त म्हणतात, कारण या प्रकरणात बाह्य वातावरणात त्याच्या वर्तनावर नियंत्रण ठेवणारी कोणतीही माहिती नसते.

हे देखील पहा:

पीएलसीच्या वापराच्या उदाहरणावर इलेक्ट्रिकल अभियांत्रिकीमध्ये मायक्रोप्रोसेसर सिस्टमचा वापर

लॉजिक मॉड्यूल लोगो! औद्योगिक ऑटोमेशनसाठी