इलेक्ट्रोमॅग्नेट्सचे कर्षण बल

इलेक्ट्रोमॅग्नेट ज्या बलाने फेरोमॅग्नेटिक पदार्थांना आकर्षित करते ते चुंबकीय प्रवाह F वर किंवा समतुल्यपणे, इंडक्शन B आणि इलेक्ट्रोमॅग्नेट S च्या क्रॉस-सेक्शनल क्षेत्रावर अवलंबून असते.

इलेक्ट्रोमॅग्नेटचे दाब बल सूत्राद्वारे निर्धारित केले जाते

F = 40550 ∙ B^ 2 ∙ S,

जेथे F हे इलेक्ट्रोमॅग्नेटचे दाब बल आहे, kg (बल देखील न्यूटनमध्ये मोजले जाते, 1 kg = 9.81 N किंवा 1 N = 0.102 kg); बी - प्रेरण, टी; S हे इलेक्ट्रोमॅग्नेटचे क्रॉस-सेक्शनल क्षेत्र आहे, m2.

ची उदाहरणे

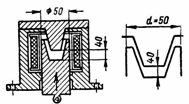
1. नल इलेक्ट्रोमॅग्नेट एक चुंबकीय सर्किट आहे (चित्र 1). जर चुंबकीय प्रेरण B = 1 T असेल आणि इलेक्ट्रोमॅग्नेटच्या प्रत्येक ध्रुवाचे क्रॉस-सेक्शनल क्षेत्र S = 0.02 m2 (Fig. 1, b) असेल तर, हॉर्सशो क्रेन इलेक्ट्रोमॅग्नेटची उचलण्याची शक्ती किती आहे? इलेक्ट्रोमॅग्नेट आणि आर्मेचरमधील अंतराच्या प्रभावाकडे दुर्लक्ष करा.

तांदूळ. 1. इलेक्ट्रोमॅग्नेट उचलणे

F = 40550 ∙ B^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0.02 = 1622 kg.

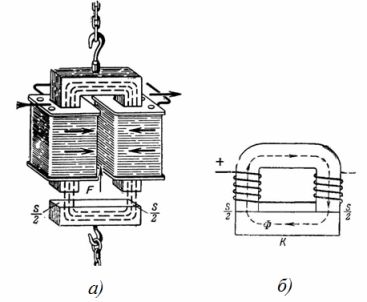
2. गोलाकार स्टील इलेक्ट्रोमॅग्नेटमध्ये अंजीरमध्ये दर्शविलेले परिमाण आहेत. 2, a आणि b. इलेक्ट्रोमॅग्नेटची उचलण्याची शक्ती 3 T आहे. इलेक्ट्रोमॅग्नेट कोरचे क्रॉस-सेक्शनल क्षेत्र निश्चित करा, n. p. आणि चुंबकीय प्रवाह I = 0.5 A वर कॉइलच्या वळणांची संख्या.

तांदूळ. 2. गोल इलेक्ट्रोमॅग्नेट

चुंबकीय प्रवाह गोलाकार आतील गाभ्यातून जातो आणि दंडगोलाकार शरीरातून परत येतो. कोर Sc आणि केसिंग Sk चे क्रॉस-सेक्शनल क्षेत्रे अंदाजे समान आहेत, म्हणून कोर आणि केसिंगमधील इंडक्शन व्हॅल्यू व्यावहारिकदृष्ट्या समान आहेत:

Sc = (π ∙ 40 ^ 2) / 4 = (3.14 ∙ 1600) / 4 = 1256 cm2 = 0.1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3.14 / 4 ∙ (5184-3600) = 1243.5 cm2 = 0.12435 m2;

S = Sc + Sk = 0.24995 m2 ≈0.25 m2.

इलेक्ट्रोमॅग्नेटमधील आवश्यक प्रेरण F = 40550 ∙ B^ 2 ∙ S या सूत्राद्वारे निर्धारित केले जाते.

जेथे B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0.25)) = 0.5475 T.

या इंडक्शनमधील व्होल्टेज कास्ट स्टीलच्या चुंबकीकरण वक्र वर आढळते:

एच = 180 ए / मी.

फील्ड लाइनची सरासरी लांबी (Fig. 2, b) lav = 2 ∙ (20 + 23) = 86 सेमी = 0.86 मी.

चुंबकीय शक्ती I ∙ ω = H ∙ lav = 180 ∙ 0.86 = 154.8 Av; I = (I ∙ ω) / I = 154.8 / 0.5 = 310 A.

प्रत्यक्षात एन. s, म्हणजेच वर्तमान आणि वळणांची संख्या अनेक पटींनी जास्त असणे आवश्यक आहे, कारण इलेक्ट्रोमॅग्नेट आणि आर्मेचरमध्ये एक अपरिहार्य हवा अंतर आहे, ज्यामुळे चुंबकीय सर्किटच्या चुंबकीय प्रतिकारात लक्षणीय वाढ होते. म्हणून, इलेक्ट्रोमॅग्नेट्सची गणना करताना हवेतील अंतर लक्षात घेतले पाहिजे.

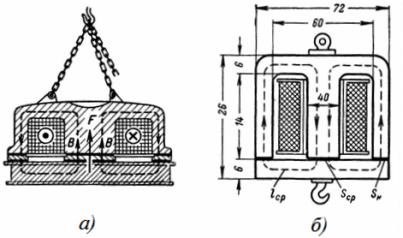
3. नळासाठी इलेक्ट्रोमॅग्नेटच्या कॉइलमध्ये 1350 वळणे आहेत, एक विद्युत् I = 12 A त्यातून वाहते. इलेक्ट्रोमॅग्नेटची परिमाणे अंजीरमध्ये दर्शविली आहेत. 3. आर्मेचरपासून 1 सेमी अंतरावर इलेक्ट्रोमॅग्नेट कोणते वजन उचलते आणि गुरुत्वाकर्षणानंतर ते किती वजन धरू शकते?

तांदूळ. 3. इलेक्ट्रोमॅग्नेटिक कॉइल

I ∙ ω सह बहुतेक N. हवेच्या अंतरातून चुंबकीय प्रवाह चालविण्यासाठी खर्च केला जातो: I ∙ ω≈Hδ ∙ 2 ∙ δ.

चुंबकीय बल I ∙ ω = 12 ∙ 1350 = 16200 A.

H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, नंतर Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02.

म्हणून, 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02, i.e. B = 1.012T.

आम्ही असे गृहीत धरतो की इंडक्शन B = 1 T आहे, कारण n चा भाग आहे. c. I ∙ ω स्टीलमध्ये चुंबकीय प्रवाह चालविण्यासाठी खर्च केला जातो.

I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс सूत्रानुसार ही गणना तपासू.

चुंबकीय रेषेची सरासरी लांबी आहे: लव = 2 ∙ (7 + 15) = 44 सेमी = 0.44 मी.

B = 1 T (10000 Gs) येथे तीव्रता Hc चुंबकीकरण वक्र वरून निर्धारित केली जाते:

Hc = 260 A/m. I ∙ ω = 0.8 ∙ B ∙ 2 + 2.6 ∙ 44 = 1.6 ∙ 10000 + 114.4 = 16114 Av.

चुंबकीय शक्ती I ∙ ω = 16114 Av एक इंडक्शन B = 1 T तयार करत आहे, हे दिलेल्या n च्या व्यावहारिकदृष्ट्या समान आहे. v. I ∙ ω = 16200 Av.

कोर आणि शंकूचे एकूण क्रॉस-सेक्शनल क्षेत्र आहे: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0.006 m2.

इलेक्ट्रोमॅग्नेट 1 सेमी अंतरावरून F = 40550 ∙ B^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0.006 = 243.3 kg वजनाचा चार्ज आकर्षित करेल.

आर्मेचर आकर्षित झाल्यानंतर हवेतील अंतर व्यावहारिकरित्या अदृश्य होत असल्याने, इलेक्ट्रोमॅग्नेट खूप मोठा भार सहन करू शकतो. या प्रकरणात, संपूर्ण एन. c. I ∙ ω फक्त स्टीलमध्ये चुंबकीय प्रवाह चालविण्यासाठी खर्च केला जातो, म्हणून I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m

अशा व्होल्टेजवर, स्टील व्यावहारिकरित्या संतृप्त होते आणि त्यातील इंडक्शन अंदाजे 2 T असते. इलेक्ट्रोमॅग्नेट आर्मेचरला F = 40550 ∙ B^ 2 ∙ S = 40550 ∙ 4 ∙ 0.07g = 0.006 k बळाने आकर्षित करते.

4. सिग्नल (ब्लिंकर) रिलेमध्ये गोल कोर असलेले आर्मर्ड इलेक्ट्रोमॅग्नेट 1 आणि वाल्व-प्रकार आर्मेचर 2 असते, जे इलेक्ट्रोमॅग्नेटला विद्युत प्रवाह पुरवल्यानंतर, ब्लिंकर 3 आकर्षित करते आणि सोडते, जे सिग्नल अंक उघडते (चित्र. 4).

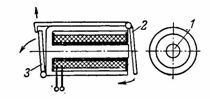
तांदूळ. 4. चिलखत इलेक्ट्रोमॅग्नेट

चुंबकीय शक्ती I ∙ ω = 120 Av आहे, हवेतील अंतर δ = 0.1 सेमी आहे आणि इलेक्ट्रोमॅग्नेटचे एकूण क्रॉस-सेक्शनल क्षेत्र S = 2 सेमी 2 आहे. रिलेच्या पुल फोर्सचा अंदाज लावा.

Inductance B हे समीकरण I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ या समीकरणाचा वापर करून अनुक्रमिक अंदाजे निर्धारित केले जाते.

चला एन. c. Hc ∙ lc 15% I ∙ ω आहे, i.e. 18 Av.

मग मी ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0.2; Hδ = 102 / 0.2 = 510 A/cm = 51000 A/m.

म्हणून आम्हाला इंडक्शन बी आढळतो:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0.0637 T.

F = 40550 ∙ B^ 2 ∙ S या सूत्रामध्ये B मूल्य बदलल्यानंतर, आपल्याला मिळते:

F = 40550 ∙ 0.0637 ^ 2 ∙ 0.0002 = 0.0326 kg.

5. डीसी ब्रेक सोलेनोइड (चित्र 5) मध्ये टॅपर्ड स्टॉपसह पिस्टन आर्मेचर आहे. आर्मेचर आणि कोरमधील अंतर 4 सेमी आहे. कार्यरत व्यास (गोलाकार संपर्क क्षेत्रासह कोर) d = 50 मिमी. आर्मेचर 50 किलोच्या शक्तीने कॉइलमध्ये खेचले जाते. बलाच्या मध्य रेषेची लांबी lav = 40 सेमी. n निश्चित करा. pp. आणि 3000 वळणे असल्यास कॉइलचा प्रवाह.

तांदूळ. 5. डीसी ब्रेक सोलेनोइड

इलेक्ट्रोमॅग्नेटच्या कार्यरत विभागाचे क्षेत्रफळ d = 5 सेमी व्यासासह वर्तुळाच्या क्षेत्राएवढे आहे:

S = (π ∙ d ^ 2) / 4 = 3.14 / 4 ∙ 25 = 19.6 cm2.

F = 50 kg बल तयार करण्यासाठी आवश्यक असलेले इंडक्शन B हे F = 40550 ∙ B^ 2 ∙ S या समीकरणावरून आढळते.

जेथे B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0.00196)) = 0.795 T.

चुंबकीय शक्ती I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

आम्ही स्टील Hc ∙ lc साठी चुंबकीय शक्ती 15% I ∙ ω आहे या वस्तुस्थितीवर आधारित, सोप्या पद्धतीने निर्धारित करतो:

I ∙ ω = 0.15 ∙ I ∙ ω + Hδ ∙ δ; 0.85 ∙ I ∙ ω = Hδ ∙ δ; 0.85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0.795 ∙ 0.04) / 0.85 = 30,000 Av.

चुंबकीय प्रवाह I = (I ∙ ω) / ω = 30000/3000 = 10 A.